Math
This section contains the following pages:
Basic
- Abs
- AbsFract32
- Adder
- AdderFract32
- AdderInt32
- Ceil
- Divide
- Exp
- Floor
- Fmod
- Frexp
- Ldexp
- Log
- Log10
- Log10Fract32
- Log2
- Log2Fract32
- Modf
- MultiplierV2
- MultiplierV2Fract32
- Pow10toX
- Pow2Fract32
- Pow
- PowFract32
- Reciprocal
- ReciprocalFract32
- Remainder
- Round
- ShiftFract32
- Sign
- Sqrt
- SqrtFract32
- Square
- SquareAdd
- SquareAddFract32
- SquareFract32
- Subtract
- SubtractFract32
- SubtractInt32
- SumDiff
- SumDiffFract32
- SumDiffInt32
Basic Math
These modules perform basic math operations.
 | Adder | Adds signals |
 | Subtract | Subtracts signals |
 | Multiplier | Multiplies signals |
 | Divide | Divides signals |
 | Reciprocal | Computes 1/x |
The Adder and Subtract module by default have two input pins. Additional pins can be specified on the module properties. For the Adder, all inputs are summed together. For the Subtract module, the last input pin is subtracted from the others. The Adder and Subtract modules both handle signals with multiple input channels.
The Adder module has an additional argument that can be selected on the module properties:
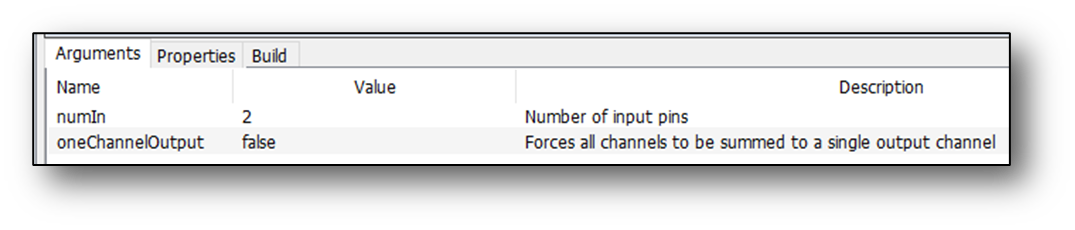
When oneChannelOutput is set to true then the output will be mono and all input channels will be summed together to form the output. In this mode, the input pins can have different numbers of channels. By default, oneChannelOutput is set to false and all input pins have to have the same number of channels and the output will be multichannel as well. A useful way of using the Adder is to sum together the left and right components of a stereo signal. The traditional way is to use a Deinterleave module
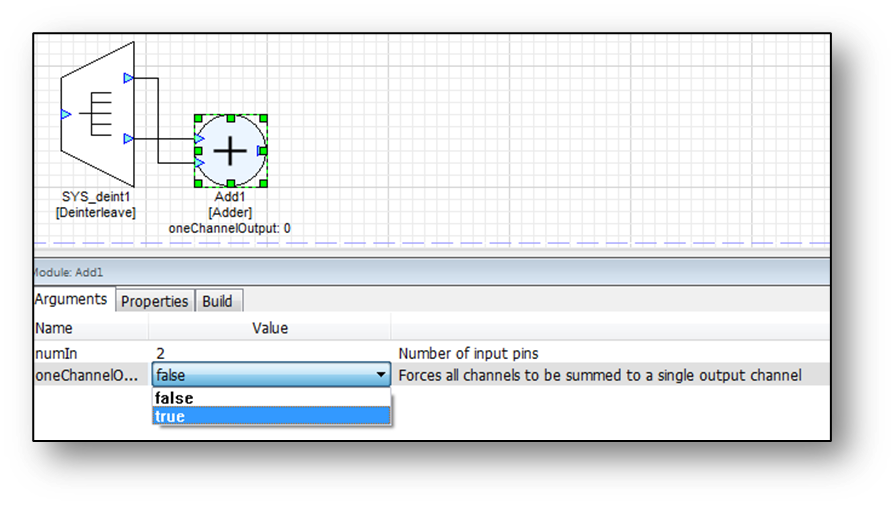
Or, use an Adder module with the number of input pins set to 1 and oneChannelOutput checked:
In addition to these basic math functions, the Math folder has modules corresponding to the functions in the standard C math.h library. These modules will be skipped, but here is a preview:
DB Conversion
To convert to and from dB10 and dB20, this folder hosts Approx and exact modules. The Approx modules are less cpu intensive, and less accurate. To be clear, the UndB modules convert from dB to linear scaling.
Lookup Tables
The Table Interp module uses a table with clickable/movable points to discern how the input values scale into the output pin. For data in between the points, the scaling is interpolated either linearly or cubicly.
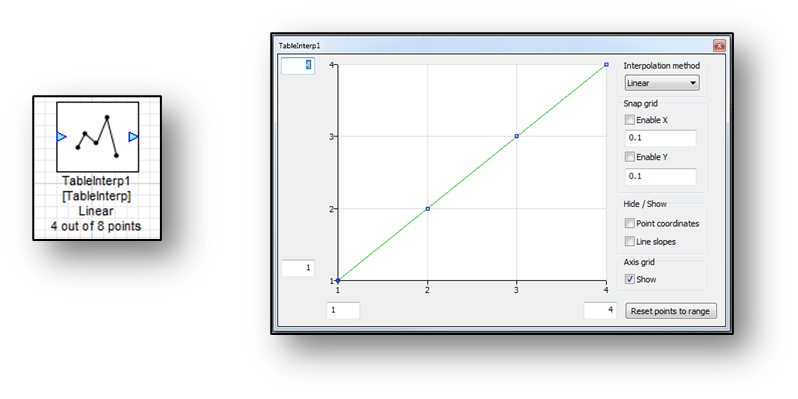
Table Interp2d takes in a vector input (x and y pins) and scales them according to the nPoints length matrix. It uses bilinear interpolation of the table values at the four neighboring points (above, below, left, right).
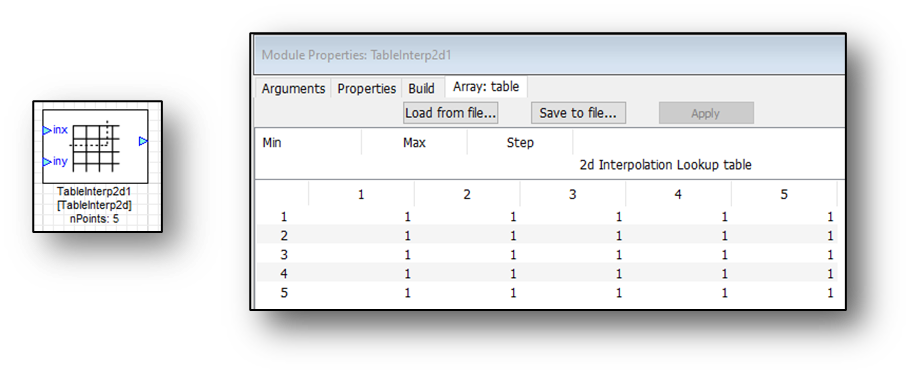
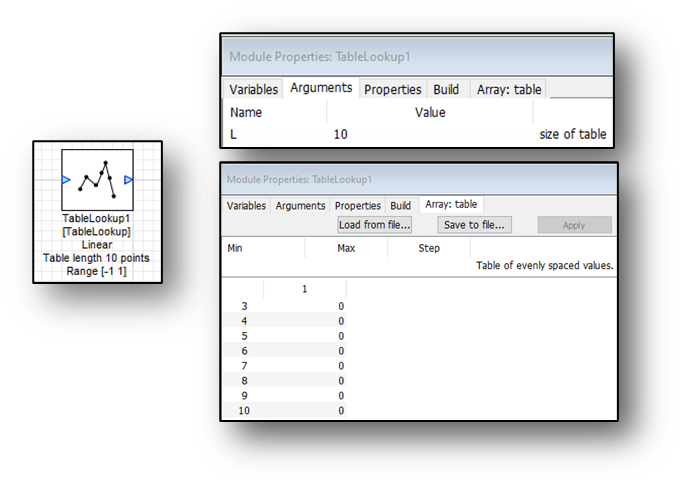
TableLookup uses either Linear or nearest interpolation. The user has to specify the upper and lower bounds of this table. Set the size of the table with the ‘L’ variable found in the arguments:
For non-interpolated lookup tables, an integer index is listed, and output is based on that index’s data value. That data can be float or int type data.
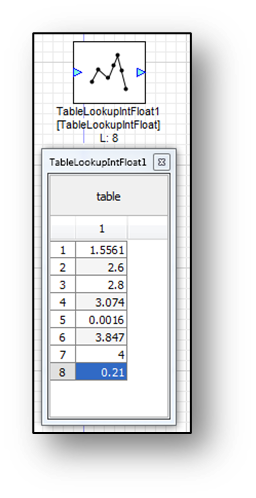
TableLookupIntFloat
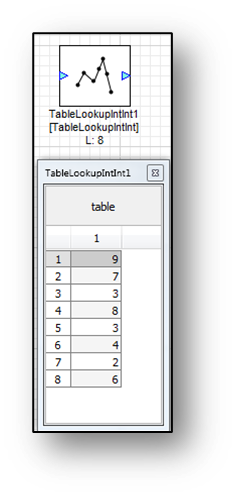
TableLookupIntInt
Nonlinearities
Modules which implement point nonlinearities and are stateless and easy to understand. They are listed below and used in the examples later on.
 | ClipAsym | Hard clipper |
 | Polynomial | Polynomial f(x) |
 | Square | Squares a signal x*x |
Other nonlinearities which are documented elsewhere are the Abs, TableInterp, SoftClip, and TwoPieceInterp modules.
Trig
Trig functions are simple enough to not need much detail. They operate in radians, not degrees. The following trig functions are provided:

Advanced Math
The advanced math modules include the functions seen below:
The Convolve module is similar to the FIR module, with the property that it can ignore signal tails. It is normally not used for filtering. Its shape parameter acts as a truncation control. When the user selects shape 0, no truncating occurs, outputting normal convolution. If the user selects shape 1, the module will ignore the first N/2 samples of the output, then display the next N samples, followed by ignoring the last N/2 samples. This is useful for statistics between two data sets. This is essentially partial correlation.
The Correlate module is similar to the convolve module, except it differs in the order of the output.
Derivative and Integral modules compute discrete derivative and integral equations respectively:
y[n] = 1/dt * (x[n] - x[n-1])
where dt is the time step, dt = 1/SR.
y[n] = dt/K * sum(x[0] .. x[n])
where dt is the time step, dt = 1/SR and K is a gain.
